CAP 理论

什么是 CAP 定理

在理论计算机科学中，CAP 定理（CAP theorem），又被称作布鲁尔定理（Brewer's theorem），它指出对于一个分布式计算系统来说，不可能同时满足以下三点：

一致性（Consistency）：等同于所有节点访问同一份最新的数据副本。
可用性（Availability）：每次请求都能获取到非错的响应（但是不保证获取的数据为最新数据）。
分区容错性（Partition tolerance）：以实际效果而言，分区相当于对通信的时限要求。系统如果不能在时限内达成数据一致性，就意味着发生了分区的情况，必须就当前操作在 C 和 A 之间做出选择。

根据定理，分布式系统只能满足三项中的两项而不可能满足全部三项。

理解 CAP 理论的最简单方式是想象两个节点分处分区两侧。允许至少一个节点更新状态会导致数据不一致，即丧失了 C 性质。如果为了保证数据一致性，将分区一侧的节点设置为不可用，那么又丧失了 A 性质。除非两个节点可以互相通信，才能既保证 C 又保证 A，这又会导致丧失 P 性质。

CAP 定理起源于加州大学柏克莱分校的计算机科学家埃里克·布鲁尔在 2000 年的分布式计算原理研讨会（PODC）上提出的一个猜想。在 2002 年，麻省理工学院的赛斯·吉尔伯特和南希·林奇发表了布鲁尔猜想的证明，使之成为一个定理。

吉尔伯特和林奇证明的 CAP 定理比布鲁尔设想的某种程度上更加狭义。定理讨论了在两个互相矛盾的请求到达彼此连接不通的两个不同的分布式节点的时候的处理方案。

分布式系统中，多个节点之间的网络本来是连通的，但是因为某些故障（比如部分节点网络出了问题）某些节点之间不连通了，整个网络就分成了几块区域，这就叫 网络分区。

当发生网络分区时，如果我们要继续服务，那么强一致性和可用性只能 2 选 1。也就是说当网络分区之后 P 是前提，决定了 P 之后才有 C 和 A 的选择。也就是说分区容错性我们是必须要实现的。简而言之就是：CAP 理论中分区容错性是一定要满足的，在此基础上，只能满足可用性或者一致性。

因此，分布式系统理论上不可能选择 CA 架构，只能选择 CP 或者 AP 架构。比如 ZooKeeper、HBase 就是 CP 架构，Cassandra、Eureka 就是 AP 架构，Nacos 不仅支持 CP 架构也支持 AP 架构。

若系统出现网络分区，系统中的某个节点在进行写操作。为了保证 C，必须要禁止其他节点的读写操作，这就和 A 发生冲突了。如果为了保证 A，其他节点的读写操作正常的话，那就和 C 发生冲突了。因此不可能选择 CA 架构。如果网络分区正常，也就说不需要保证 P 的时候，C 和 A 能够同时保证。

选择 CP 架构还是 AP 架构的关键在于当前的业务场景，没有定论，比如对于需要确保强一致性的场景如银行一般会选择 CP 架构。

下图是 Dubbo 的架构图。注册中心 Registry 负责服务地址的注册与查找，相当于目录服务，服务提供者和消费者只在启动时与注册中心交互，注册中心不转发请求，压力较小。

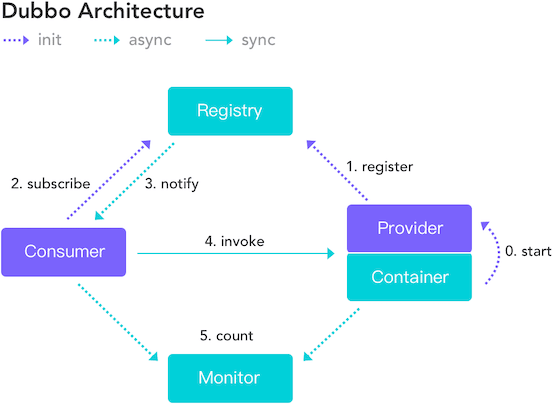
常见的可以作为注册中心的组件有：ZooKeeper、Eureka、Nacos 等。

ZooKeeper 保证的是 CP：任何时刻对 ZooKeeper 的读请求都能得到一致性的结果，但是，ZooKeeper 不保证每次请求的可用性。比如在 Leader 选举过程中或者半数以上的机器不可用的时候服务就是不可用的。
Eureka 保证的则是 AP：Eureka 在设计的时候就是优先保证 A（可用性）。在 Eureka 中不存在什么 Leader 节点，每个节点都是一样的、平等的。因此 Eureka 不会像 ZooKeeper 那样出现选举过程中或者半数以上的机器不可用的时候服务就是不可用的情况。Eureka 保证即使大部分节点挂掉也不会影响正常提供服务，只要有一个节点是可用的就行了。只不过这个节点上的数据可能并不是最新的。
Nacos 不仅支持 CP 也支持 AP。